Shape

class arlunio.shape.Circle(*args, **kwds)[source]

Inputs:

width: int height: int

Bases:

X Y

Produces:

Mask
../_images/basic-circle.png

We define a circle using the following equality.

\[(x - x_c)^2 + (y - y_c)^2 = r^2\]
xc

Corresponds with the \(x_c\) variable in the equation above and defines the \(x\)-coordinate of the circle’s center.

yc

Corresponds with the \(y_c\) variable in the equation above and defines the \(y\)-coordinate of the circle’s center.

r

Corresponds with the \(r\) variable in the equation above and defines the radius of the circle.

pt

If None, then all points within the radius of the circle will be considered to be part of it. If this is set to some positive number then all points between radii (1 - pt) * r and (1 + pt) * r will be considered part of the circle.

Examples

../_images/target.png

Combining a few circles we’re able to draw a target:

import arlunio as ar
import arlunio.image as image
import arlunio.shape as shape

@ar.definition
def Target(width: int, height: int) -> image.Image:
    img = image.new((width, height), color="white")
    parts = [
        (shape.Circle(pt=0.02), "#000"),
        (shape.Circle(r=0.75, pt=0.12), "#f00"),
        (shape.Circle(r=0.6, pt=0.05), "#f00"),
        (shape.Circle(r=0.4), "#f00"),
    ]

    for part, color in parts:
        img = image.fill(
            part(width=width, height=height), foreground=color, image=img
        )

    return img

target = Target()
img = target(width=1920, height=1080)

Making use of the xc and yc attributes we can produce an approximation of the olympics logo

../_images/olympic-rings.png 
import arlunio as ar
import arlunio.image as image
import arlunio.shape as shape

@ar.definition
def OlympicRings(width: int, height: int, *, spacing=0.5, pt=0.025):

    dy = spacing / 4
    dx = spacing / 2
    args = {"scale": 0.5, "r": spacing, "pt": pt}

    img = image.new((width, height), color="white")
    rings = [
        (shape.Circle(yc=dy, xc=-(2.2 * dx), **args), "#0ff"),
        (shape.Circle(yc=dy, **args), "#000"),
        (shape.Circle(yc=dy, xc=(2.2 * dx), **args), "#f00"),
        (shape.Circle(yc=-dy, xc=-(1.1 * dx), **args), "#ff0"),
        (shape.Circle(yc=-dy, xc=(1.1 * dx), **args), "#0f0")
    ]

    for ring, color in rings:
        img = image.fill(
            ring(width=width, height=height), foreground=color, image=img
        )

    return img

rings = OlympicRings()
img = rings(width=1920, height=1080)
class arlunio.shape.Ellipse(*args, **kwds)[source]

Inputs:

width: int height: int

Bases:

X Y

Produces:

Mask
../_images/simple-ellipse.png

An ellipse can be defined using the following equality.

\[\left(\frac{x - x_c}{a}\right)^2 + \left(\frac{y - y_c}{b}\right)^2 = r^2\]
xc

Corresponds with the \(x_c\) variable in the equation above and defines the \(x\)-coordinate of the ellipse’s center.

yc

Corresponds with the \(y_c\) variable in the equation above and defines the \(y\)-coordinate of the ellipse’s center.

r

Corresponds with the \(r\) variable in the equation above and controls the overall size of the ellipse.

a

Corresponds with the \(a\) variable in the equation above and controls the width of the ellipse.

b

Corresponds with the \(b\) variable in the equation above and controls the height of the ellipse.

pt

If None then all points within the radius of the ellipse will be considered to be part of it. If this is set to some positive number then all points between radii (1 - pt) * r and (1 + pt) * r will be considered part of the ellipse.

Examples

a and b together determine the overall shape of the ellipse. Increasing the value of a will stretch the ellipse width wise, increasing b has a similar effect for the height. It’s worth noting that it’s the ratio of these 2 values rather than their absolute values that has a greater effect on the shape of the ellipse. If a = b then the equation simplifies to that of a circle

../_images/ellipse-demo.png 
import arlunio as ar
import arlunio.image as image
import arlunio.shape as shape

@ar.definition
def EllipseDemo(width: int, height: int):
    img = image.new(width, height, color="white")
    ellipses = [
        shape.Ellipse(xc=-0.5, yc=-0.5, a=0.5, b=0.5, r=0.4),
        shape.Ellipse(yc=-0.5, a=1, b=0.5, r=0.4),
        shape.Ellipse(xc=0.5, yc=-0.5, a=2, b=0.5, r=0.4),
        shape.Ellipse(a=1, b=1, r=0.4),
        shape.Ellipse(xc=0.5, yc=0.5, a=2, b=2, r=0.4),
        shape.Ellipse(xc=-0.5, a=0.5, b=1, r=0.4),
        shape.Ellipse(xc=-0.5, yc=0.5, a=0.5, b=2, r=0.4)
    ]

    for ellipse in ellipses:
        img = image.fill(ellipse(width=1920, height=1080), image=img)
    return img

demo = EllipseDemo()
img = demo(width=1920, height=1080)
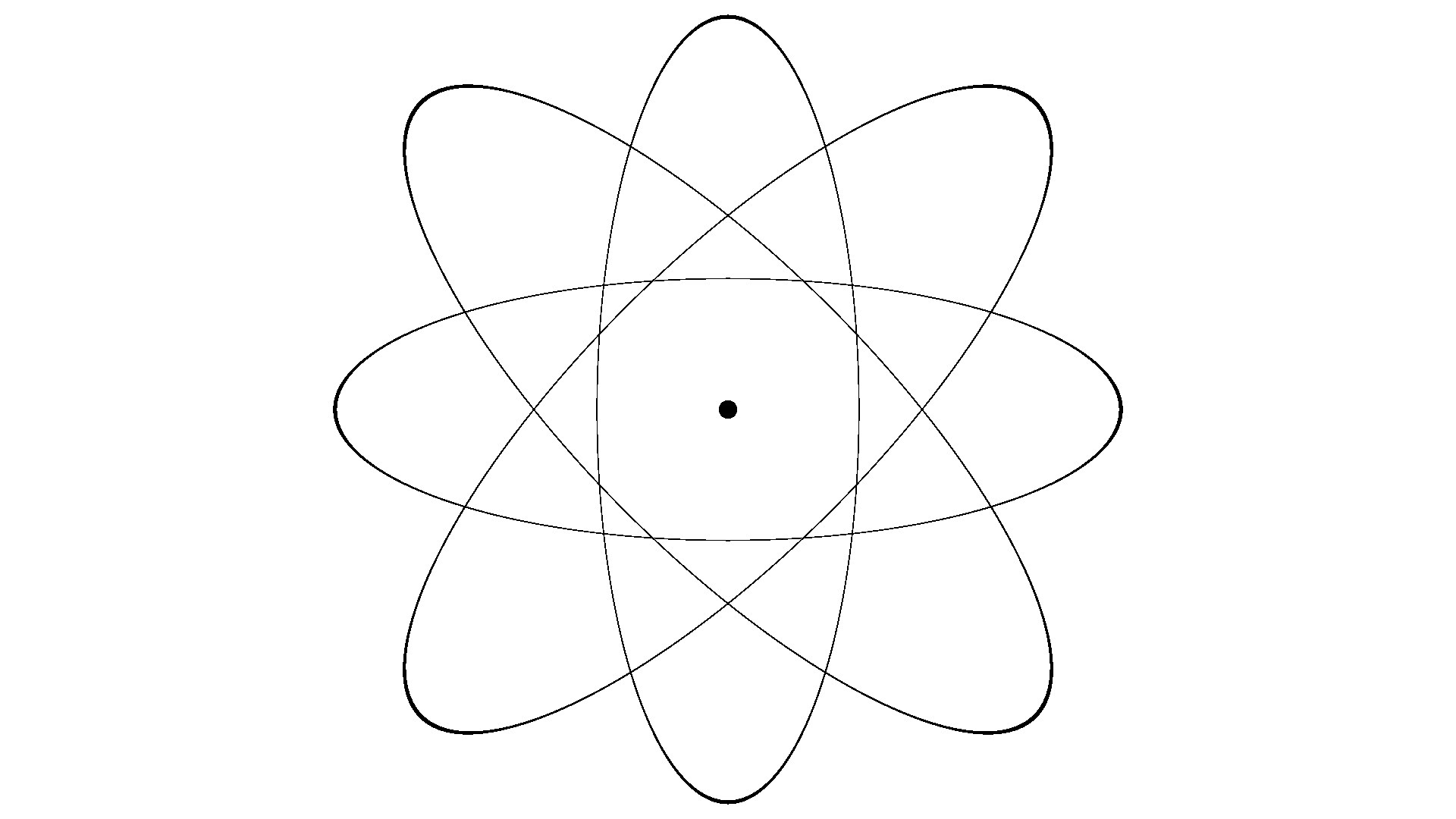
../_images/atom.png

Playing around with the values and the coordinate inputs it’s possible to draw something that looks like a diagram of an atom:

import arlunio as ar
import arlunio.image as image
import arlunio.math as math
import arlunio.shape as shape

@ar.definition
def Atom(x: math.X, y: math.Y):
    img = None

    ellipses = [
        (shape.Ellipse(a=1.5, b=0.5, pt=0.005), x, y),
        (shape.Ellipse(a=1.5, b=0.5, r=1, pt=0.005), x + y, y - x),
        (shape.Ellipse(a=0.5, b=1.5, pt=0.005), x, y),
        (shape.Ellipse(a=1.5, b=0.5, r=1, pt=0.005), x - y, x + y),
        (shape.Ellipse(a=1, b=1, r=0.15), x, y)
    ]

    bg = "white"

    for ellipse, ex, ey in ellipses:
        img = image.fill(ellipse(x=ex, y=ey), image=img, background=bg)
        bg = None

    return img

atom = Atom()
img = atom(width=1920, height=1080)
class arlunio.shape.Rectangle(*args, **kwds)[source]

Inputs:

width: int height: int

Bases:

X Y

Produces:

Mask
../_images/simple-rectangle.png

A rectangle:

xc

Defines the \(x\)-coordinate of the center of the rectangle

yc

Defines the \(y\)-coordinate of the center of the rectangle

size

Defines the area of the rectangle

ratio

Defines the ratio of the width to the height of the rectangle

pt

If None then all points within the rectangle’s border will be considered to be part of it. If set to some positive number then all points within (1 - pt) * size to (1 + pt) * size of the border will be considered to be part of the rectangle.

Examples

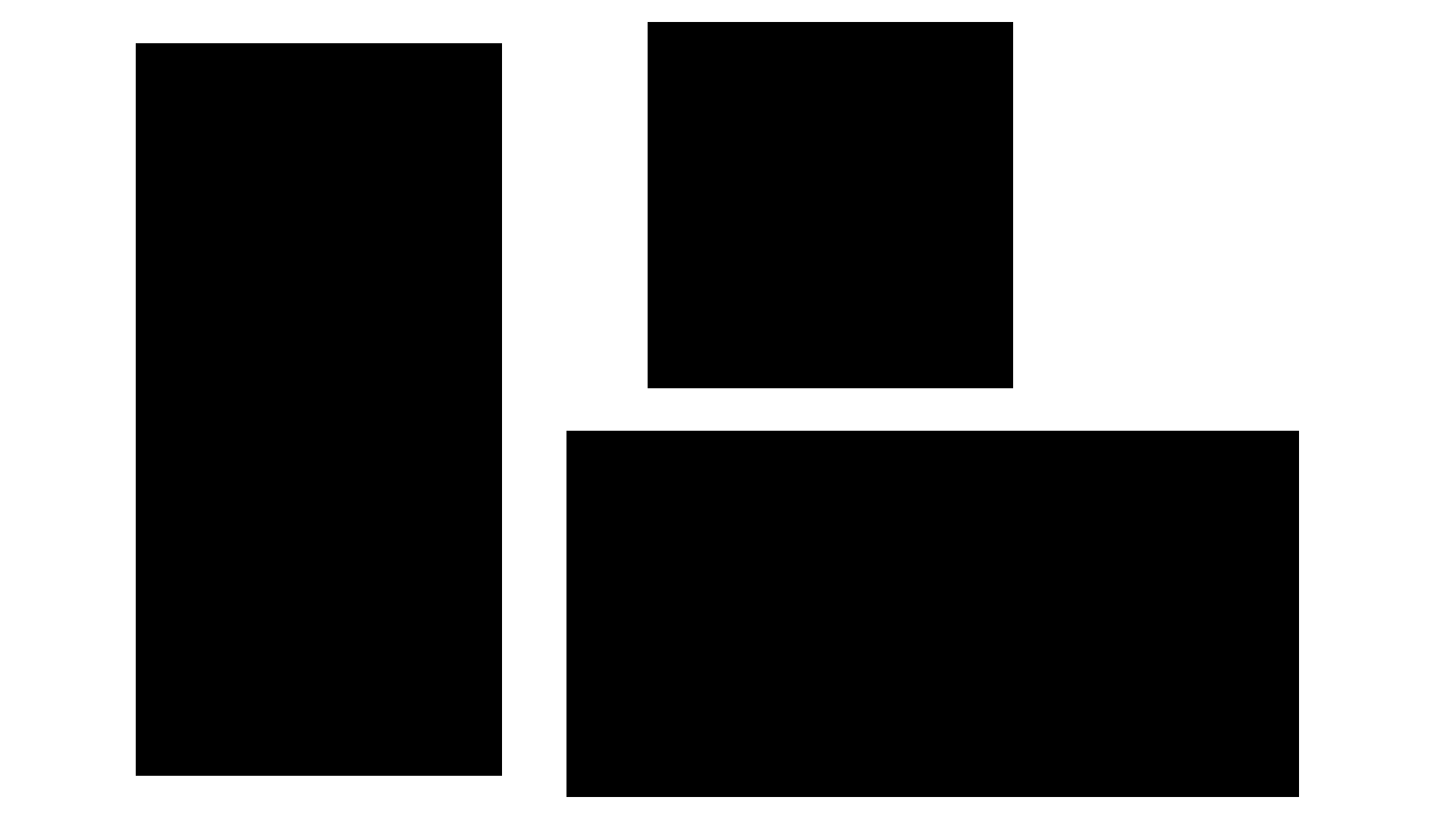
../_images/rectangle-demo.png 
import arlunio as ar

from arlunio.shape import Rectangle
from arlunio.image import fill

@ar.definition
def RectangleDemo(width: int, height: int):
    image = None
    rects = [
        Rectangle(xc=-1, size=0.4, ratio=0.5),
        Rectangle(xc=0.25, yc=0.5, size=0.2, ratio=1),
        Rectangle(xc=0.5, yc=-0.5, size=0.4, ratio=2)
    ]

    for r in rects:
        image = fill(r(width=width, height=height), image=image)

    return image

demo = RectangleDemo()
image = demo(width=1920, height=1080)
class arlunio.shape.Square(*args, **kwds)[source]

Inputs:

width: int height: int

Bases:

X Y

Produces:

Mask
../_images/simple-square.png

A square:

xc

Defines the \(x\)-coordinate of the square’s center

yc

Defines the \(y\)-coordinate of the square’s center

size

Defines the size of the square, sides will have a length of 2 * size

pt

If None then all points within the square’s border will be considered to be part of it. If set to some positive number then all points within (1 - pt) * size to (1 + pt) * size of the border will be considered to be part of the square.

Example

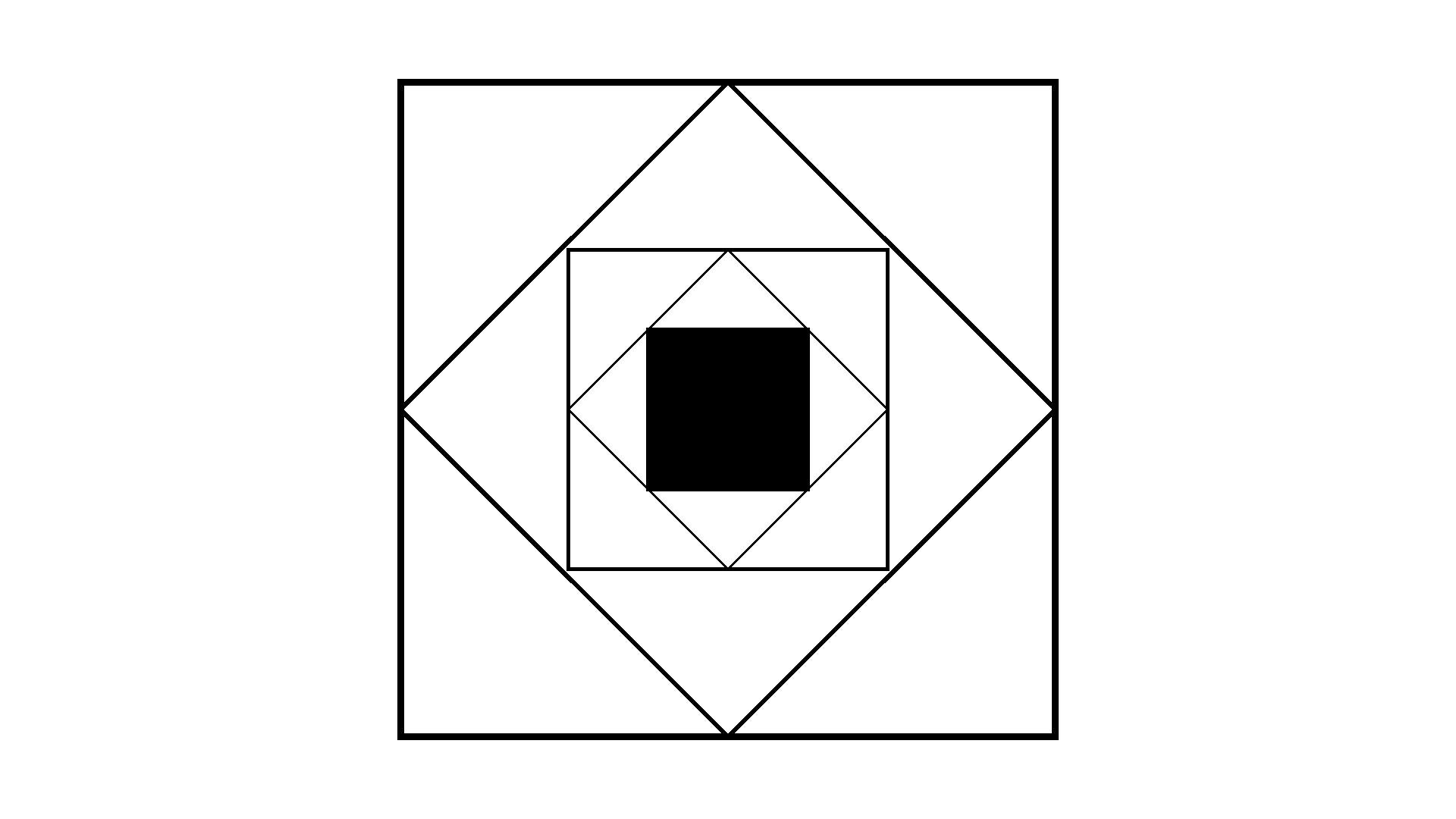
../_images/square-demo.png 
import arlunio as ar
import arlunio.image as image
import arlunio.math as math
import arlunio.shape as shape

@ar.definition
def SquareDemo(x: math.X, y: math.Y):
    img = None
    squares = [
        (shape.Square(pt=0.01), x, y),
        (shape.Square(pt=0.01), x + y, x - y),
        (shape.Square(size=0.39, pt=0.01), x, y),
        (shape.Square(size=0.39, pt=0.01), x + y, x - y),
        (shape.Square(size=0.2), x, y),
    ]

    bg = "white"

    for square, sx, sy in squares:
        img = image.fill(square(x=sx, y=sy), image=img, background=bg)
        bg = None

    return img

square = SquareDemo()
img = square(width=1920, height=1080)
class arlunio.shape.SuperEllipse(*args, **kwds)[source]

Inputs:

width: int height: int

Bases:

X Y

Produces:

Mask
../_images/superellipse.png

We define a SuperEllipse by the following equality.

\[\left|\frac{(x - x_c)}{a}\right|^n + \left|\frac{(y - y_c)}{b}\right|^m = r\]
xc

Corresponds with the \(x_c\) variable in the equation above and defines the \(x\)-coordinate of the center of the super ellipse.

yc

Corresponds with the \(y_c\) variable in the equation above and defines the \(y\) -coordinate of the center of the super ellipse.

r

Corresponds with the \(r\) variable in the equation above and controls the size of the super ellipse.

a

Corresponds with the \(a\) variable in the equation above and controls the width of the super ellipse.

b

Corresponds with the \(b\) variable in the equation above and controls the height of the super ellipse.

n

Corresponds with the \(n\) variable in the equation above and controls the profile of the curve far from \(x = 0\)

m

Corresponds with the \(m\) variable in the equation above and controls the profile of the curve close to \(x = 0\). If m = None (default) then it will be set to the value of n.

pt

If None then all points within the radius of the super ellipse will be considered to be part of it. If this is set to some positive number then all points between radii (1 - pt) * r and (1 + pt) * r will be considered part of the super ellipse.

Examples

Being a generalisation of the regular arlunio.shape.Ellipse definition most of the attributes will have a similar effect on the outcome so be sure to check it out for additional examples. For the SuperEllipse definition the most interesting attributes are n and m greatly affect the shape of the super ellipse.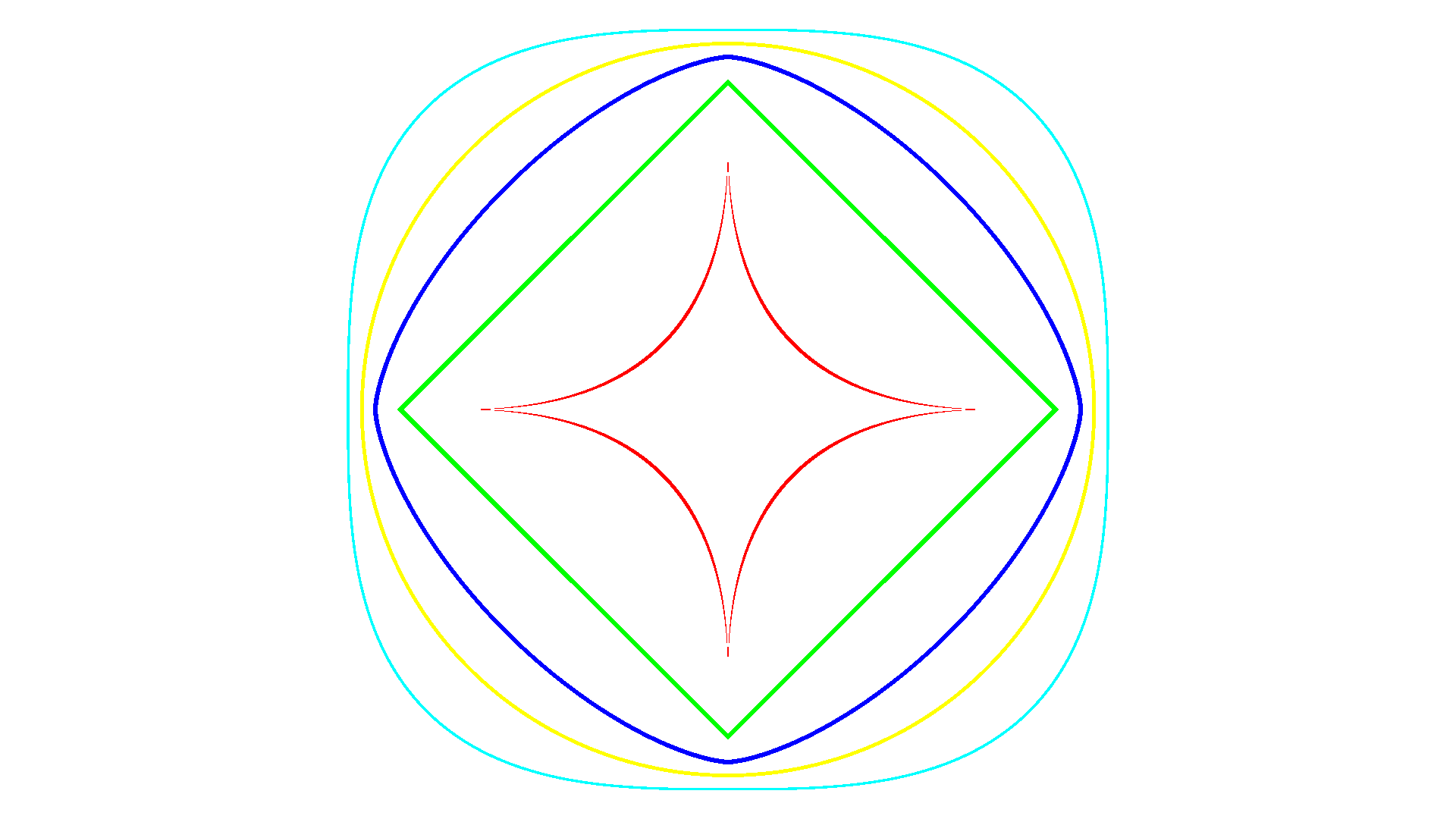

../_images/superellipse-demo.png 
import arlunio as ar
import arlunio.image as image
import arlunio.shape as shape

@ar.definition
def SuperEllipseDemo(width: int, height: int):
    img = image.new(width, height, color="white")
    ellipses = [
        (shape.SuperEllipse(n=0.5, pt=0.01),'#f00'),
        (shape.SuperEllipse(n=1, pt=0.01),'#0f0'),
        (shape.SuperEllipse(n=1.5, pt=0.01), '#00f'),
        (shape.SuperEllipse(n=2, pt=0.01), '#ff0'),
        (shape.SuperEllipse(n=3, pt=0.01), '#0ff')
    ]

    for ellipse, color in ellipses:
        img = image.fill(
            ellipse(width=1920, height=1080), foreground=color, image=img
        )

    return img

demo = SuperEllipseDemo()
img = demo(width=1920, height=1080)

By default if you don’t specify a value for m it will inherit the value assigned to n. However if you set m to a different value then you can get even more interesting results!

../_images/eye-of-sauron.png

“Eye of Sauron”:

import arlunio as ar
import arlunio.image as image
import arlunio.shape as shape


@ar.definition
def Sauron(width: int, height: int):
    img = image.new(width, height, color="white")
    ellipses = [
        (shape.SuperEllipse(a=2, n=3, m=0.2, r=0.98),'#f00'),
        (shape.SuperEllipse(n=2),'#f50'),
        (shape.SuperEllipse(n=0.1, m=2), '#000'),
    ]

    for ellipse, color in ellipses:
        img = image.fill(
            ellipse(width=1920, height=1080), foreground=color, image=img
        )

    return img

eye = Sauron()
img = eye(width=1920, height=1080)
class arlunio.shape.Triangle(*args, **kwds)[source]

Inputs:

width: int height: int

Bases:

Barycentric

Produces:

Mask

A triangle.

../_images/triangle-demo.png